4. Contenedoras de dos Dimensiones: Matrices

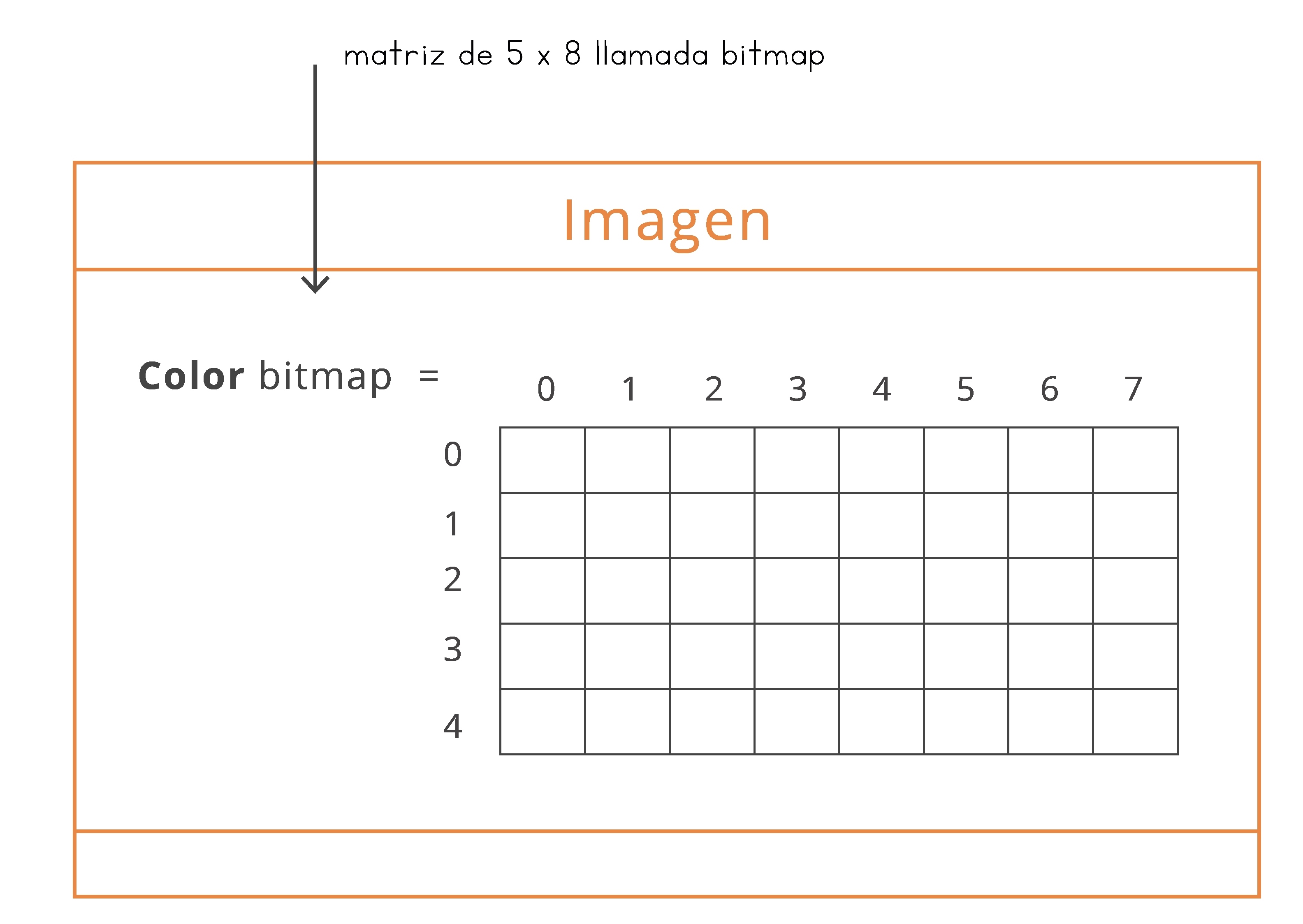
Una matriz es una estructura contenedora de dos dimensiones, de tamaño fijo, cuyos elementos son referenciados utilizando dos índices: el índice de la fila y el índice de la columna. Este tipo de estructuras se utiliza cuando en el mundo del problema hay características que se adaptan a esta representación bidimensional. Para hacer el paralelo con la visualización que usamos en el nivel 3 para mostrar la idea de un arreglo, en la figura 6.4 presentamos una manera de imaginar una clase que tiene un atributo que corresponde a una matriz.

Fig. 6.4 Visualización de una matriz como un atributo de una clase

En las secciones que siguen, veremos la manera de declarar, crear y manipular contenedoras de dos dimensiones de tamaño fijo en el lenguaje de programación Java.

4.1. Declaración de una Matriz

En Java, las estructuras contenedoras de dos dimensiones de tamaño fijo se denominan matrices y se declaran como se muestra en el ejemplo 1.

Ejemplo 1

Objetivo: Mostrar la manera de declarar una matriz en Java.

En este ejemplo se presenta la declaración en Java de la matriz que representa la imagen en el caso de estudio.

public class Imagen
{
    //--------------------------------------
    // Atributos
    //--------------------------------------

    private int ancho;

    private int alto;

    private Color[][] bitmap;
}

Es conveniente declarar el número de columnas (ancho) y el número de filas (ancho) como atributos. Esto va a facilitar realizar posteriores modificaciones al programa.

La declaración del atributo bitmap indica que es una matriz de dos dimensiones de tamaño fijo (el valor exacto del tamaño será determinado en el momento de la inicialización de la matriz) y cuyos elementos son todos de tipo Color.

La clase Color es una clase predefinida de Java que permite manejar colores en formato RGB. Esta clase de encuentra en el paquete java.awt. En nuestros ejemplos utilizamos algunos de los servicios que ofrece esa clase.

4.2. Inicialización de una Matriz

Al igual que con cualquier otro atributo de una clase, es necesario inicializar la matriz antes de poderla utilizar. Para hacerlo, se deben definir las dimensiones de la matriz. Esta inicialización es obligatoria, puesto que es entonces cuando le decimos al computador cuántos valores se van a manejar en la matriz, lo que corresponde al espacio en memoria que debe reservar. Veamos en el ejemplo 2 cómo se hace esto para el caso de estudio.

Ejemplo 2

Objetivo: Mostrar la manera de crear una matriz en Java.
En este ejemplo se presenta el constructor de la clase Imagen, que tiene la responsabilidad de crear la matriz que va a contener los píxeles.

// Constructor    
//--------------------------------------    
public Imagen( )    
{
    ancho = 400;
    alto = 300;
    bitmap = new Color[ alto ][ ancho ];
}

Se utiliza la instrucción new, pero en este caso se indican dos dimensiones de la matriz, en nuestro caso de ejemplo 300 filas (alto) cada una con 400 columnas (ancho).
Aunque el espacio ya queda reservado con la instrucción new, el valor de cada uno de los elementos del arreglo sigue siendo indefinido. Esto lo arreglaremos más adelante. Recuerde que siempre van primero las filas y luego las columnas.

El lenguaje Java provee un operador especial (length), que permite consultar el número de filas que tiene una matriz. En el caso de ejemplo, la expresión bitmap.length debe dar el valor 300 que corresponde al número de filas, independientemente de si las casillas individuales ya han sido o no inicializadas. De la misma manera el operador length nos permite preguntar el número de columnas de la matriz. La expresión bitmap[0].length debe dar el valor 400, que corresponde al número de columnas en la fila 0. Como en nuestro caso todas las filas tienen el mismo número de columnas, esa expresión nos puede servir para establecer la segunda dimensión de la matriz.

4.3. Acceso a los Elementos de una Matriz

Para acceder a una posición de una matriz necesitamos dos índices, uno para indicar la fila y el otro para indicar la columna (por ejemplo, con la sintaxis bitmap[5][6] hacemos referencia al elemento de la casilla que está en la fila 5 en la columna 6). Recuerde que un índice es un valor entero y sus valores van desde 0 hasta el número de elementos de la dimensión correspondiente menos 1. Para tomar o modificar el valor de un elemento particular de una matriz necesitamos dar los dos índices. El siguiente ejemplo inicializa todos los elementos de bitmap en la clase Imagen con el color azul.

public void imagenAzul( )
{
    for( int i = 0; i < alto; i++ )
    {
        for( int j = 0; j < ancho; j++ )
        {
            bitmap[ i ][ j ] = new Color( 0, 0, 255 );
        }
    }
}

Este método recorre la matriz inicializando las casillas con objetos de la clase Color cuyo valor representa el azul.
Debemos saber que el color azul en el formato RGB se representa por los valores 0, 0, 255.
Con la sintaxis bitmap[ i ][ j ] hacemos referencia a la casilla que se encuentra en la fila i columna j.
Fíjese que en cada casilla queda una referencia a un objeto distinto de la clase Color (120.000 objetos distintos, si la imagen es de 300 x 400).

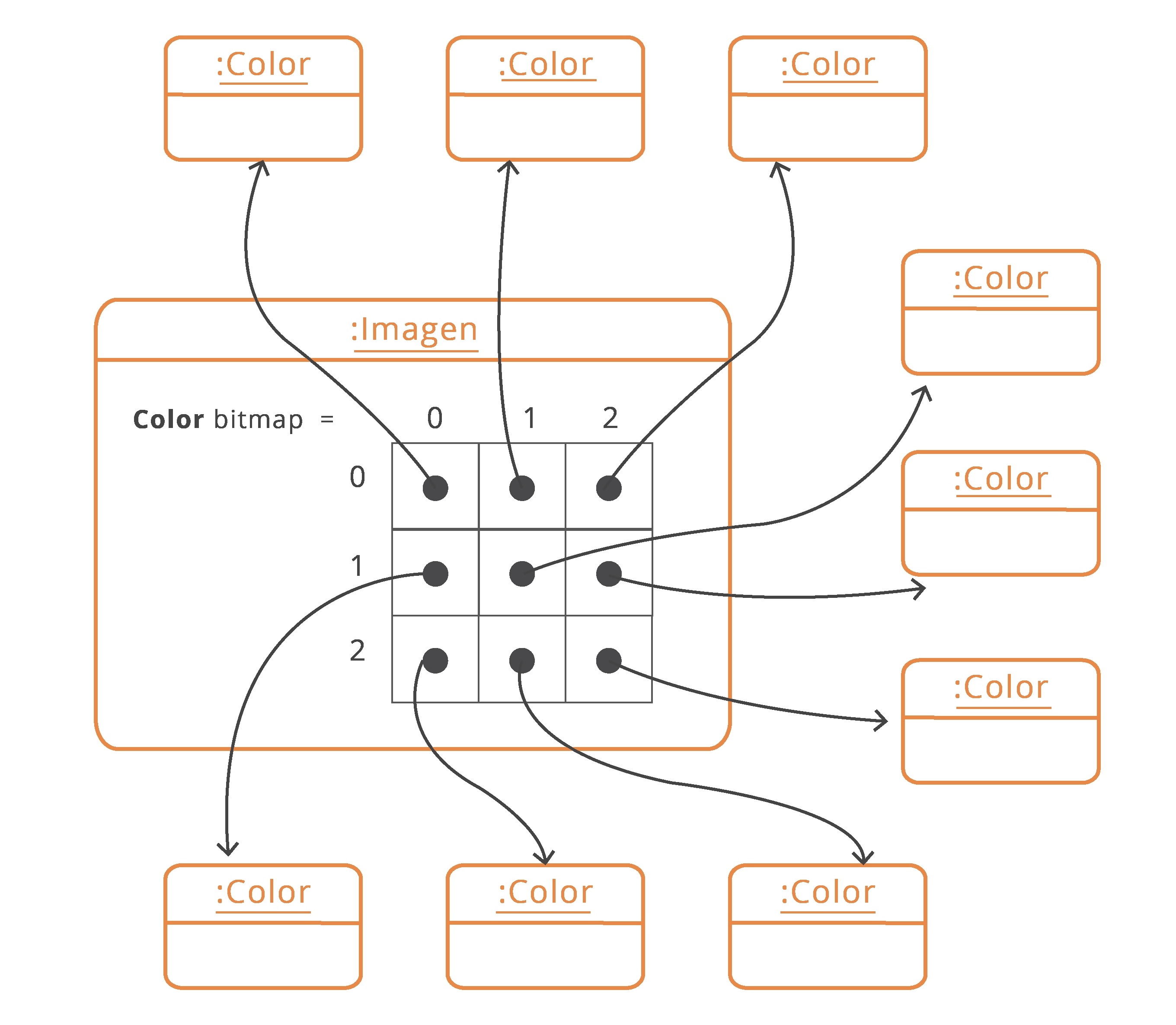
En la figura 6.5 se muestra el diagrama de objetos después de haber ejecutado el método anterior, suponiendo que la imagen es de 3 x 3.

Fig. 6.5 Diagrama de objetos para una imagen completamente azul de 3 x 3

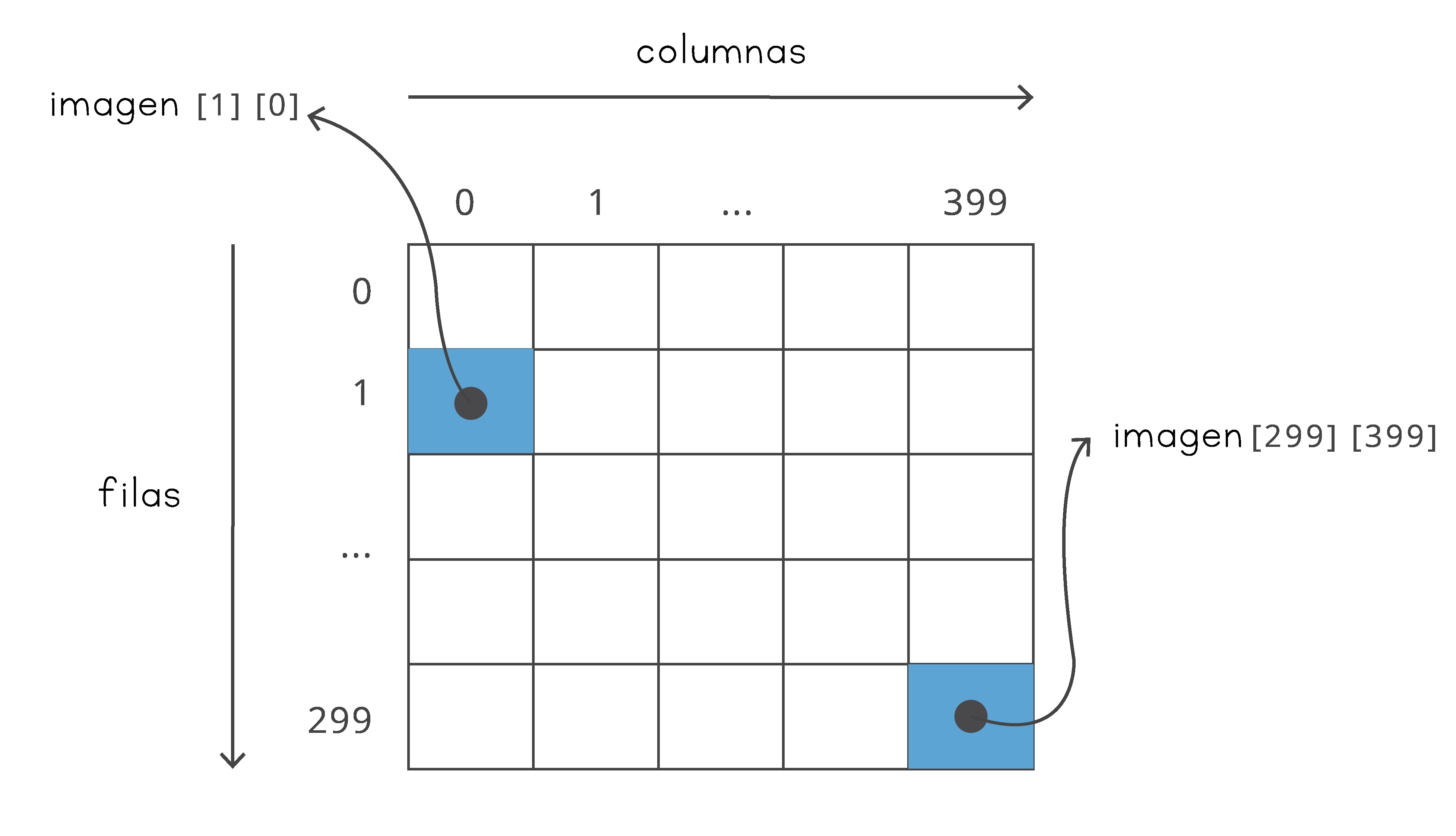
Note que en el método del ejemplo anterior con el primer ciclo recorremos las filas empezando por la correspondiente al índice cero y terminando en la fila alto-1 (vamos de arriba hacia abajo recorriendo las filas, como se muestra en la figura 6.6). Una vez que se fija una fila, el segundo ciclo nos permite recorrer las columnas de esa fila. Este recorrido se hace desde la columna 0 hasta la columna ancho-1. Note que cada vez que se termina con una fila, el ciclo interior vuelve a ejecutarse desde el principio e inicializa la columna en cero.

Fig. 6.6 Recorrido de la matriz con la imagen

El algoritmo anterior también se podría escribir utilizando la instrucción while, como se presenta a continuación:

public void imagenAzul( )
{
    int i = 0;

    while( i < alto )
    {
        int j = 0;

        while( j < ancho )
        {
            bitmap[ i ][ j ] = new Color( 0, 0, 255 ); 
            j++;
        }

        i++;
    }
}

Este método hace la misma inicialización del ejemplo anterior, pero utiliza la instrucción while en lugar de la instrucción for.
Con el índice i recorremos las filas, mientras que con el índice j recorremos las columnas.
Dentro del ciclo interno, recorremos todas las columnas de la fila i (allí j va cambiando para pasar por todas las columnas de la matriz).
En la condición del primer ciclo podría remplazarse el atributo alto por bitmap.length. Ambas expresiones hacen referencia al número de filas de la matriz.

En la sintaxis de acceso a un elemento se pasa primero la fila en la que se encuentra y después la columna. Tanto las filas como las columnas se comienzan a numerar desde cero.

Cuando dentro de un método tratamos de acceder a una casilla con un par de índices no válidos (al menos uno de ellos es menor que 0 o mayor que el máximo índice permitido para la dimensión correspondiente), obtenemos el error de ejecución: java.lang.ArrayIndexOutOfBoundsException

4.4. Comparar los Elementos de una Matriz

Si los elementos de una matriz son de un tipo simple (enteros, reales, etc.), se comparan utilizando el operador == que estudiamos en el segundo nivel. Después de todo, el estar almacenados en una matriz no cambia el hecho de que sean valores simples, y por lo tanto se deben seguir manipulando de la misma manera que hemos venido utilizando hasta ahora.

Cuando se trata de referencias a objetos hay que tener un poco más de cuidado. Si utilizamos el operador == estamos preguntando si las dos referencias señalan al mismo objeto físico y, a veces, no es eso lo que queremos saber. Para establecer si son iguales, aunque no estén referenciando el mismo objeto, se utiliza el método equals: piense por ejemplo que dos objetos pueden representar el color azul sin necesidad de ser el mismo objeto. Esta idea se ilustra en ejemplo 3. Si miramos un poco hacia atrás, esa es la razón por la cual siempre hemos comparado las cadenas de caracteres utilizando dicho método, en lugar del operador ==. No nos importa que estén referenciando el mismo objeto, sino que contengan la misma cadena de caracteres.

Ejemplo 3

Objetivo: Mostrar la manera de comparar los elementos de una matriz, cuando dichos elementos son objetos.

En este ejemplo se muestra la diferencia entre comparar dos referencias a objetos utilizando el operador == y el método equals. También se ilustra la consecuencia de asignar a una variable una referencia a un objeto que ya está en una casilla de una matriz.

Comenzamos este ejemplo mostrando un diagrama de objetos con una imagen de 2 x 3, cuya primera fila está coloreada de rojo (255,0,0) y la segunda de azul (0,0,255).
Cada casilla tiene un objeto diferente que representa el color que allí aparece.
La expresión bitmap[0][0] == bitmap[0][1] es falsa. Ambas referencias llevan a objetos que representan el color rojo, pero son objetos distintos.
La expresión bitmap[0][0].equals(bitmap[0][1]) es verdadera. Ambas referencias llevan a objetos que representan el color rojo y el método no tiene en cuenta que sean instancias distintas.
La expresión bitmap[0][0].equals(bitmap[1][0]) es falsa. El primer objeto representa el color rojo, mientras que el segundo representa el color azul.
Si hacemos la siguiente asignación: Color temp = bitmap[0][0], tenemos que tanto la variable temp como la casilla de coordenadas 0,0 referencian el mismo objeto. En ese caso la comparación temp == bitmap[0][0] es verdadera, lo mismo que la expresióntemp.equals(bitmap[0][0]).

El método equals() no está definido de manera adecuada en todas las clases. Algunas como String o Color sí lo tienen. Otras (como por ejemplo las que hemos desarrollado a lo largo de este libro), no lo tienen bien definido y si vamos a usar el método con esas clases nos tocaría implementarlo.

En este punto podemos retomar de nuevo la discusión planteada en la sección 4.3 sobre la imagen completamente azul: en vez de los miles de objetos para representar los píxeles (todos de color azul), ¿es posible utilizar un solo objeto con dicho fin? ¿Es posible que las 120.000 casillas de la matriz referencien todas el mismo objeto? La respuesta es que en este caso es posible, pero que dicha aproximación no se puede generalizar. En este caso lo podemos hacer porque la clase Color no tiene ningún método que permita a sus instancias modificar su valor. Si alguien quiere cambiar el color de un píxel debe crear un nuevo objeto de esa clase para representarlo. Esto tiene como consecuencia que, en el caso de estudio, sí podemos compartir el objeto azul de la clase Color desde todos los puntos de la imagen, ya que nadie puede cambiarlo. Si existiera un método en dicha clase que permitiera, por ejemplo, hacer más rojo un color, el hecho de utilizar un solo objeto compartido por todos haría que al cambiar de color un solo píxel, el cambio se traslade a todos los otros píxeles de la imagen que están siendo representados por el mismo objeto.

Tarea 1

Objetivo: Ilustrar la manera de escribir un algoritmo para manipular una matriz.

Complete el siguiente método de la clase Imagen. No olvide que para preguntar si dos colores son iguales, se debe utilizar el método equals de la clase Color.

/** 
*   Devuelve el número de píxeles en la imagen cuyo color es el dado como parámetro.
*   @param pColorBuscado Objeto por el que se quiere preguntar. pColorBuscado != null.
*   @return Número de puntos en la matriz cuyo color es igual al dado.
*/
public int cuantosPixelColor( Color pColorBuscado )
{









}

4.5. Patrones de Algoritmo para Recorrido de Matrices

Las soluciones de muchos de los problemas que debemos resolver sobre matrices son similares entre sí y obedecen a ciertos esquemas ya conocidos. En esta sección pretendemos adaptar algunos de los patrones que estudiamos en el nivel 3 al caso de las matrices. De nuevo, lo ideal es que al leer un problema que debemos resolver (el método que debemos escribir), podamos identificar el patrón al cual corresponde y utilizar las guías que existen para resolverlo. Eso simplificaría enormemente la tarea de escribir los métodos que tienen ciclos y que trabajan sobre estructuras de matrices.

4.5.1. Patrón de Recorrido Total

Este patrón se aplica en las situaciones donde debemos recorrer todos los elementos que contiene la matriz para lograr la solución. En el caso de estudio de la imagen tenemos varios ejemplos de esto:

Contar cuántos puntos en la imagen son de color rojo.
Cambiar el color de todos los puntos en la imagen haciéndolos más oscuros.
Cambiar cada color de la imagen por su negativo.
Contar cuántos puntos en la imagen tienen la componente roja distinta de cero.

Para la solución de cada uno de esos problemas, se requiere siempre un recorrido de toda la matriz para poder cumplir el objetivo que se está buscando. Un primer ciclo para recorrer las filas y, luego, un ciclo por cada una de ellas para recorrer sus columnas.

Para lograr el recorrido total, tenemos que:

El índice para iniciar el primer ciclo debe empezar en cero.
La condición para continuar es que el índice sea menor que el número de filas de la matriz.
El avance consiste en sumarle uno al índice.
El cuerpo del segundo ciclo contiene el recorrido de las columnas y debe ser tal que (a) el índice debe comenzar en cero, (b) la condición para continuar es que el índice sea menor que el número de columnas de la matriz, (c) el avance consiste en sumarle uno al índice. Esa estructura que se repite en todos los algoritmos que necesitan un recorrido total es lo que denominamos el esqueleto del patrón, el cual se puede resumir con el siguiente fragmento de código:

for( int i = 0; i < NUM_FILAS; i++ )
{
    for( int j = 0; j < NUM_COLUMNAS; j++ )
    {
        <cuerpo del ciclo>
    }
}

El patrón consiste en dos ciclos anidados: el primero para recorrer las filas, el segundo para recorrer las columnas de cada fila.

Lo que cambia en cada caso es lo que se quiere hacer en el cuerpo del ciclo. Aquí hay dos variantes principales. En la primera, todos los elementos de la matriz van a ser modifiados siguiendo alguna regla (por ejemplo, oscurecer el color de todos los puntos). Lo único que se hace en ese caso es remplazar el cuerpo del ciclo en el esqueleto por las instrucciones que hacen la modificación pedida para un elemento de la matriz. Damos un ejemplo de aplicación en el siguiente código (método de la clase Imagen), que oscurece una imagen:

for( int i = 0; i < alto; i++ )
{
    for( int j = 0; j < ancho; j++ )
    {
        bitmap[ i ][ j ] = bitmap[ i ][ j ].darker();
    }
}

Partimos del esqueleto del patrón. Sólo cambiamos el cuerpo del segundo ciclo, para explicar la manera de modificar cada una de las casillas de la matriz.
Toda modificación que hagamos allí para la casilla de coordenadas i, j, la estaremos haciendo para cada uno de los elementos de la estructura.
El método darker() crea una nueva instancia de la clase Color, más oscura que el objeto que recibe la llamada.

La segunda variante del patrón es cuando se quiere calcular alguna propiedad sobre el conjunto de elementos de la matriz (por ejemplo, contar cuántos puntos tienen el componente rojo igual a cero). Como vimos en el nivel 3, esta variante implica cuatro decisiones que definen la manera de completar el esqueleto del patrón:

Cómo acumular la información que se va llevando a medida que avanza el segundo ciclo.
Cómo inicializar dicha información.
Cuál es la condición para modificar dicho acumulado en el punto actual del ciclo.
Cómo modificar el acumulado. Veamos esos puntos para resolver el problema de contar cuántos puntos tienen el componente rojo igual a cero.

¿Cómo acumular información? Vamos a utilizar una variable de tipo entero llamada cuantosRojoCero que va llevando el número de puntos que tienen el componente rojo en cero.

¿Cómo inicializar el acumulado? La variable cuantosRojoCero se debe inicializar en 0, antes de la primera iteración del ciclo exterior.

¿Condición para cambiar el acumulado? Cuando el método getRed() del objeto Color que se encuentra en bitmap[i][j] sea igual a 0.

¿Cómo modificar el acumulado? El acumulado se modifica incrementándolo en 1.

El método resultante es el siguiente:

public int rojoCero( )
{
    int cuantosRojoCero = 0;

    for( int i = 0; i < alto; i++ )
    {
        for( int j = 0; j < ancho; j++ )
        {
            if( bitmap[ i ][ j ].getRed( ) == 0 )
            {
                cuantosRojoCero++;
            }
        }
    }

    return cuantosRojoCero;
}

Este método de la clase Imagen permite calcular el número de píxeles de la imagen cuyo componente rojo es cero.
El método getRed() de la clase Color retorna el índice de rojo que tiene el objeto sobre el que se invoca el método. En este caso corresponde al color del objeto que se encuentra referenciado en la casilla (i,j).
Si dicho método retorna el valor 0, debemos incrementar la variable en la que vamos acumulando el resultado.

Tarea 2

Objetivo: Generar habilidad en el uso del patrón de recorrido total para escribir un método que manipula una matriz.

Escriba los métodos de la clase Imagen que resuelven los siguientes problemas, que corresponden a las dos variantes del patrón de algoritmo de recorrido total.

Escriba un método que modifique los puntos de la matriz convirtiéndolos en sus negativos. El negativo se calcula restándole 255 a cada componente RGB del color y tomando el valor absoluto del resultado.

public void negativoImagen( )
{









}

Escriba un método que indique cuál es la tendencia de color de la imagen. Esto se calcula de la siguiente manera: un píxel tiene un color de tendencia roja, si su índice es mayor que los otros dos. Lo mismo sucede con los demás colores. Este método retorna 0 si la imagen no tiene ninguna tendencia, 1 si la tendencia es roja, 2 si la tendencia es verde y 3 si la tendencia es azul.

public int calcularTendencia( )
{














}

4.5.2. Patrón de Recorrido Parcial

Como vimos con los arreglos y con los vectores, algunos problemas de manejo de estructuras contenedoras no exigen recorrer todos los elementos para lograr el objetivo propuesto. Piense por ejemplo en el problema de saber si hay algún punto negro (0, 0, 0) en la imagen. En ese caso hacemos un recorrido que puede terminar cuando encontremos el primer punto negro o cuando lleguemos al final de la matriz sin haberlo encontrado. Un recorrido parcial se caracteriza porque existe una condición que debemos verificar en cada iteración para saber si debemos detener el ciclo o volverlo a repetir.

En este patrón debemos tener en cuenta la condición de salida de la siguiente manera:

boolean termino = false;

for( int i = 0; i < NUM_FILAS && !termino; i++ )
{

    for( int j = 0; j < NUM_COLUMNAS && !termino; j++ )
    {
        <cuerpo del ciclo>

        if( <problema terminado> ) 
        {
            termino = true;
        }   
    }
}

Este esqueleto es una variante del que utilizamos en el caso de los arreglos, con la diferencia de que utilizamos la variable termino para hacerlo salir de los dos ciclos a la vez.
Tal como vimos en el nivel 3, la variable termino se puede reemplazar por cualquier condición que indique el punto en el que el problema ya ha sido resuelto.

Hay casos en los cuales se deben utilizar dos variables distintas para controlar la salida de cadauno de los ciclos de manera independiente. En ese caso se trata simplemente de aplicar el patrón de recorrido parcial de los arreglos de manera anidada, tal como se muestra en el siguiente esqueleto de algoritmo:

boolean termino1 = false;

for( int i = 0; i < NUM_FILAS && !termino1; i++ )
{

    boolean termino2 = false;

    for( int j = 0; j < NUM_COLUMNAS && !termino2; j++ )
    {
        <cuerpo del ciclo>

        if( <problema interno terminado> ) 
        {
            termino2 = true;
        }    
    }

    if( <problema externo terminado> ) 
    {
        termino1 = true;
    }    
}

Con la variable termino1 manejamos el recorrido parcial del ciclo externo. Cuando el problema que se quiere resolver con ese ciclo se da por resuelto, la variable cambia de valor y termina la instrucción repetitiva.
Con la variable termino2 hacemos lo mismo con el ciclo interno.
De nuevo, las variables termino1 y termino2 se pueden reemplazar por expresiones lógicas que determinen si el objetivo de cada ciclo ya ha sido alcanzado.

En el ejemplo 4 se ilustra el uso de los dos esqueletos de algoritmo para resolver problemas de manipulación de matrices.

Ejemplo 4

Objetivo: Mostrar dos problemas de matrices que se resuelven utilizando los dos esqueletos planteados anteriormente.

En este ejemplo se presentan dos métodos de la clase Imagen cuya solución sigue el patrón de recorrido parcial de matrices.

public boolean hayPuntoNegro( )
{
    boolean termino = false;

    for( int i = 0; i < alto && !termino; i++ )
    {
        for( int j = 0; j < ancho && !termino; j++ )
        {
            if( bitmap[ i ][ j ].equals( Color.BLACK ) )
            {
                termino = true;
            }
        }
    }

    return termino;
}

Este método nos permite saber si hay al menos un punto negro en la imagen.
En este método, la condición para dar por resuelto el problema es que se encuentre en la casilla actual (i,j) un píxel negro. Ahí sabemos que la respuesta es verdadera, y queremos salir del ciclo interno y del ciclo externo a la vez.
Si al llegar al final de todo el recorrido no hemos encontrado ningún píxel negro, debemos retornar falso.

public boolean muchasFilasConPixelNegro( )
{
    boolean termino1 = false;
    int numFilas = 0;

    for( int i = 0; i < alto && !termino1; i++ )
    {
        boolean termino2 = false;

        for( int j = 0; j < ancho && !termino2; j++ )
        {
            if( bitmap[ i ][ j ].equals( Color.BLACK ) )
            {
                numFilas++;
                termino2 = true;
            }
        }

        if( numFilas > 50 ) 
        {
            termino1 = true;
        }  
    }

    return termino1;
}

Este método indica si hay más de 50 filas en la imagen con un píxel negro.
El objetivo del ciclo exterior se cumple si se encuentran más de 50 filas con un píxel negro. La variable termino1 debe cambiar de valor en ese caso y hacer que se termine la iteración.
El objetivo del ciclo interior es encontrar un píxel negro en la fila i. Tan pronto lo encuentre, debe usar la variable termino2 para dejar de iterar.
Puesto que el problema planteado a cada ciclo termina en un momento distinto, no podemos utilizar una sola variable como habíamos hecho en el método anterior.
En lugar de retornar el valor de la variable termino1, habríamos podido retornar la expresión numFilas > 50.

Tarea 3

Objetivo: Escribir algunos métodos para manipular matrices.

Desarrolle los métodos de la clase Imagen que resuelven los siguientes problemas. En cada caso, identifique el patrón de algoritmo que va a utilizar.

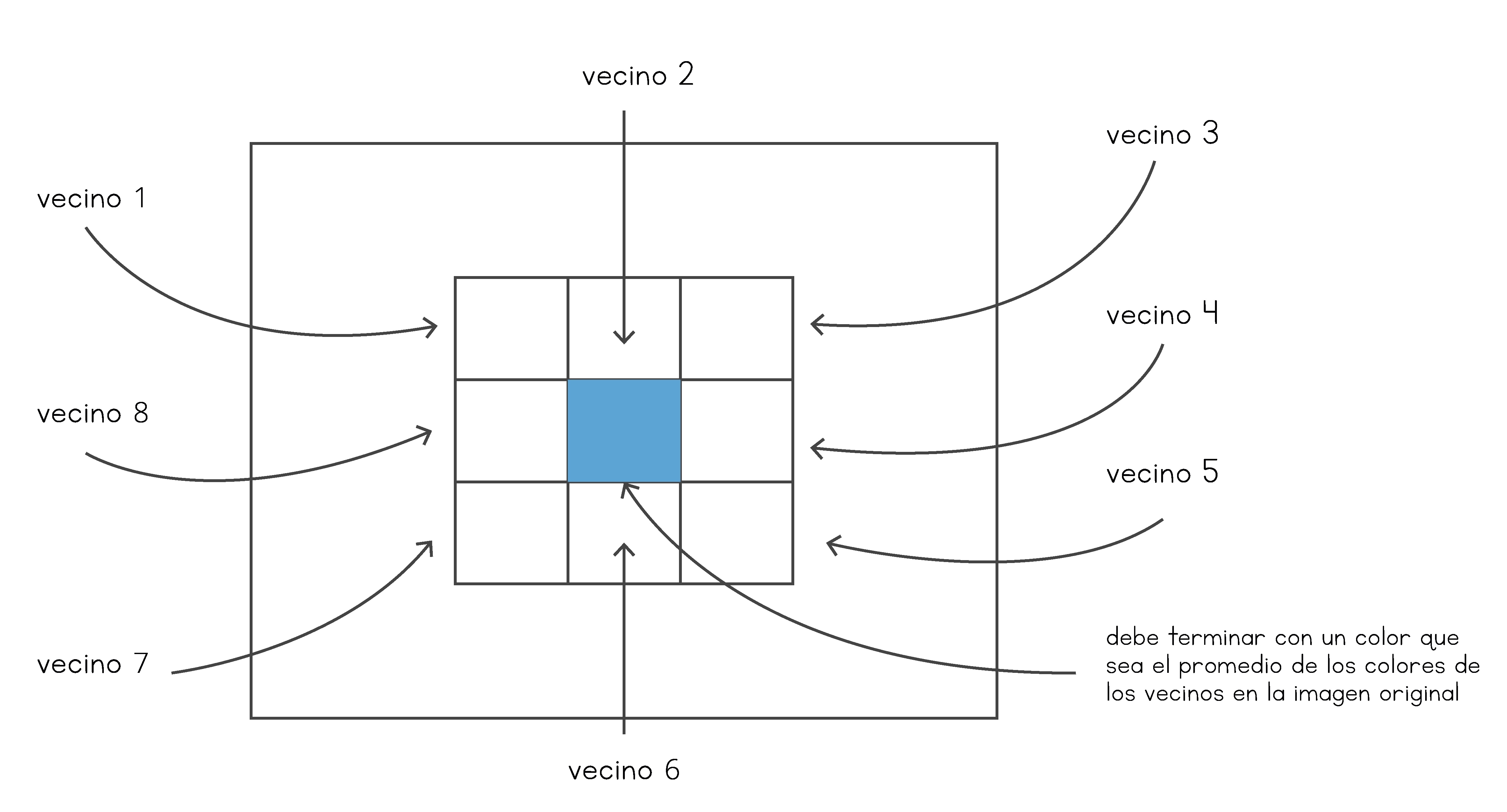
En el proceso de adquisición de una imagen, ésta puede quedar con una serie de errores los cuales hacen que se vea de mala calidad. Para corregir estos errores existe un algoritmo de filtrado, que se basa en cálcular un nuevo valor para cada píxel de la imagen. Este valor se calcula como el promedio de los 8 vecinos del píxel en la imagen original, sobre cada uno de los componentes RGB. En este proceso no se incluyen los bordes de la imagen, puesto que no tienen los 8 vecinos necesarios. Este método de la clase Imagen debe retornar una matriz con una copia de la imagen filtrada.

public Color[][] imagenFiltrada( )
{










}

En algunos contextos (en robótica, por ejemplo), en lugar del color exacto de cada píxel nos interesa solamente distinguir el fondo de la imagen (en blanco) de otros elementos que puedan aparecer (un obstáculo para el robot, por ejemplo). Escriba un método de la clase Imagen que modifique la matriz de píxeles de la siguiente manera: si la suma de los tres componentes RGB de un píxel es menor que 100, lo debe reemplazar por el color blanco (255,255,255). En caso contrario lo reemplaza por el color negro (0,0,0).

public void binarizar( )
{









}

Escriba un método de la clase Imagen que sea capaz de rotarla 90 grados a la derecha.

public void rotar90AlaDerecha( )
{









}

4.5.3. Otros Algoritmos de Recorrido

En el ejemplo 5 mostramos la manera de adaptar los patrones que hemos visto a algunos problemas típicos de manejo de matrices.

Ejemplo 5

Objetivo: Mostrar algunos problemas de matrices que pueden ser resueltos adaptando los patrones que hemos visto.

En este ejemplo se presentan tres métodos de la clase Imagen, cuya solución puede ser explicada a través de la adaptación de alguno de los patrones que hemos visto en este libro.

public int contarVerdes( int pNumFila )
{
    int numVerdes = 0;

    for( int i = 0; i < ancho; i++ )
    {
        if( bitmap[pNumFila][i].getGreen() == 255 )
        {
            numVerdes++;
        }    
    }

    return numVerdes;
}

En este método vamos a contar el número de píxeles de la fila pNumFila cuyo componente verde es el máximo posible.
En este ejemplo queremos recorrer una fila de la matriz, cuyo índice se recibe como parámetro. El hecho de utilizar una sola fila hace que pasemos al contexto de las contenedoras de una sola dimensión y que apliquemos los patrones estudiados en el nivel 3.
Aplicamos entonces el patrón de recorrido total sobre el arreglo representado por la fila dada. La única diferencia es que para indicar un elemento debemos usar la sintaxis bitmap[pNumFila][i].

public int darSumaAzulColumna( int pNumColumna )
{
    int acumAzul = 0;

    for( int i = 0; i < alto; i++ )
    {
        acumAzul += bitmap[i][pNumColumna].getBlue();
    }
    return acumAzul;
}

Este método calcula la suma del valor azul de todos los píxeles de la columna que recibe como parámetro.
Basta con ver la columna número pNmColumna como un arreglo de longitud alto (el número de filas).
Cada elemento se debe referenciar con la sintaxis bitmap[i][pNumColumna].

public boolean negroEnDiagonal( )
{
    for( int i = 0; i < alto && i < ancho; i++ )
    {
        if( bitmap[ i ][ i ].equals( Color.BLACK ) )
        {
            return true;
        }  
    }
    return false;
}

Este método indica si hay un píxel negro sobre la diagonal de la imagen que comienza en el punto (0,0).
Para este problema, vamos a imaginar el arreglo compuesto por los elementos de la diagonal: (0,0), (1,1), (2,2), etc.
Luego, aplicamos el patrón de recorrido parcial de los arreglos. La única diferencia es que, al avanzar, debemos hacerlo a la vez sobre las dos dimensiones, de manera que nos movamos por la diagonal.

Contenedoras de dos Dimensiones: Matrices